My son asked me about recursive functions yesterday morning and I showed him Dan Anderson’s online tutorial:
Even though Dan’s resource covers just about everything ( ha ha ) I thought maybe there was still something we could discuss this morning. So, I talked about the Fibonacci numbers.
First we did a quick introduction:
Next I had both boys pick their own recursively defined functions – and I got pretty lucky with the choices!
Now I showed them one approach you can use to solve these recursive equations. For the purposes of showing this idea to kids I’m not worried about the background details, but rather using the idea for some basic exponent review. (and, sorry, I’m a little careless around 1:30, but luckily catch my error fairly quickly before the whole video is derailed):
Now that we found the neat relationship between Fibonacci numbers and the golden ratio, we finished the calculation and found an explicit formula for the Fibonacci numbers:
We finished up with by checking our new formula on Mathematica. I also showed them a lucky coincidence from twitter yesterday that relates to this project. That coincidence involved this problem posted by Alexander Bogonmlny:
And this portion of the solution posted by Nassim Taleb:
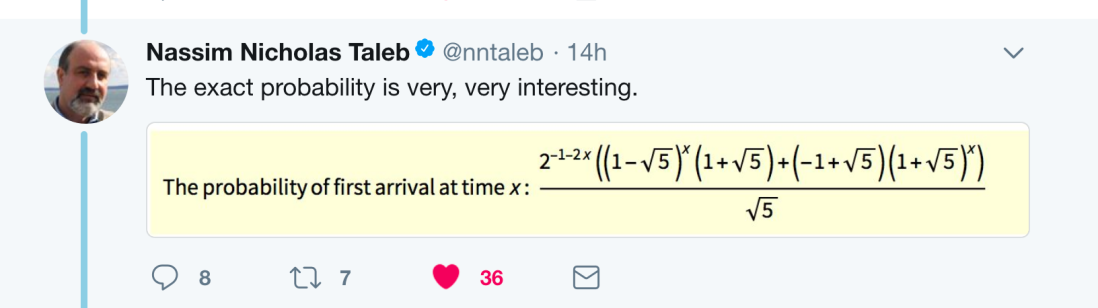
(unfortunately as I tried to zoom in on Taleb’s solution while filming the camera got way out of focus, so close your eyes for the last few minutes of this video 😦 ).
Even if the ideas for finding the explicit solution to these recursive equations is a bit advanced, I still think this is a neat topic for kids to see. It certainly is a fun way to get some nice algebra review.
