Tag: exponentials

Sharing ideas about herd immunity from Carl Bergstrom, Natalie Dean, and Tim Gowers with kids

This morning I saw a nice twitter thread about herd immunity from Tim Gowers. In that thread I learned about a NYT opinion article written by Carl Bergstrom and Natalie Dean. Here’s Gowers’s twitter thread which has a link to the article:

I thought that both the article and the twitter thread would be interesting reads for the boys this morning. We started with the article – here are a few things they found interesting:

[before diving in – our regular camera stopped working, so I filed this project with my phone. Sorry that the film quality is poor]

After talking about the article a bit, we dove into exponential growth. I think they’d understood the exponential growth ideas in the article at a high level, but going a little deeper really did help them understand the ideas about growth rates better. It was particularly interesting to hear them talk about what happens when 1 person infects 1.5 other people on average:

Next I had them read through Tim Gowers’s twitter thread (while I learned how to download videos from my phone to iMovie 🙂 ). They looked at the thread for about 10 min – here are their initial thoughts:

Finally, we took a close look at the infinite series that Gowers used in his twitter thread. My older son was already pretty familiar with infinite geometric series, but my younger son is not as used to them. Here we talked through the ideas behind the general formula for the sum. My younger son had some good ideas for how to sum the series, so this turned out to be a really worthwhile discussion:

This project was really fun. I’m glad that so many scientists and mathematicians are sharing their ideas with the public. I’m especially thankful for ideas that are presented so clearly that they can be understood by middle and high school kids.

Talking with kids about log-linear plots to help them better understand how the corona virus is spreading

I’ve seen an a lot of log-linear plots about the corona virus. My guess is that these plots are a little confusing to kids so I thought I’d spend 20 min tonight talking about them with my kids.

We started by just talking about what exponential graphs were. My younger son had a little misconception, so I was extra glad that we were having the conversation:

Next we talked about how an exponential graph changes when you switch from a regular graph to a log-linear graph:

So, with this very short introduction we took a look at two graphs about the corona virus that I’ve seen in the last week. The first was in a tweet from Steven Strogatz:

Here’s what the boys had to say about these two graphs:

Finally, we wrapped up by taking a look at some work by Dirk Brockman and co. I learned about this work here:

This tool allows us to look at the spread of the corona virus in countries all over the world. The plots are presented in log-linear form. You’ll see from this video that the boys seem to have a decent handle on what these plots are saying:

Sharing two of Patrick Honner’s calculus ideas with my son

I’ve been looking forward to sharing two calculus ideas from Patrick Honner with my son for the last week. We were, unfortunately, a little rushed when we sat down and there are a couple of mistakes in the videos below. Even though things didn’t go perfectly, I really enjoyed talking through these ideas.

Here’s the first idea – a twist on integration by parts that Honner learned from the British mathematician Tim Gowers:

Here’s the second idea – a fun surprise when a student made a creative substitution in a integration problem:

So, I stared the project by talking about how to integrate arctangent without using integration by parts:

In the last video we found a possibly surprising connection between arctan(x) and ln(x). Here I introduced the integral from the 2nd Patrick Honner tweet above and showed my son how you solve that integral using partial fractions. The point here wasn’t so much the integral, but rather to show that ln(x) showed up in an integral similar to the one we looked at in the first part of the project:

How I showed the technique that Honner’s student used (though I goofed up the substitution, unfortunately, using u = ix rather than x = iu. By dumb luck, that mistake doesn’t completely derail the problem because it only introduces an incorrect minus sign):

Now that we’ve found two connections between arctan(x) and ln(x), we went to Mathematica to see if the two anti-derivatives were really the same. It turns out the are (!) and we got an even bigger surprise when we found that Mathematica uses the same technique that Patrick Honner’s student used 🙂

Also, in this video I find a new way to introduce a minus sign by reversing the endpoints of an integral . . . . .

Talking about derivatives of exponential functions

My older son is starting the section in Stewart’s Calculus book on exponential functions. We’ve already spent a couple of days talking about inverse functions and the topic for today was finding derivatives of exponential functions.

I started by asking how he thought you’d even approach trying to find the derivative of an exponential function. It has been a while since we’ve talked about derivatives, so it took a few minutes before he came to the idea of using the definition of the derivative. Once we began to approach the problem via the definition of the derivative, we found that finding the derivative of an exponential function came down to a single limit:

Next we went to Mathematica to see if we could make any sense of this limit. Without realizing it, I had an error in the code that was causing the code to output numerical approximations. My son noticed the error and had me fix it. Unfortunately fixing that error spoiled the surprise in the answer . . . whoops 😦

Now we went back to the board to finish our computations for the derivative of an exponential function. It is pretty neat to see that the derivatives of all exponential functions are related to each other in a fairly simply way.

This was a fun discussion. The follow up discussion later was a neat problem from Stewart that asked you to show that:

e^x > 1 + x + x^2 / 2! + \ldots x^n / n! for every n. That problem was a nice exercise in derivatives of exponential functions and also techniques of proof.

Using an AB Calculus question as a estimation problem for kids

Last night I was curious what the AP calculus questions looked like and was flipping through the multiple choice questions from the 2012 AB calculus exam.

This one caught my eye because I felt that the wrong choices weren’t selected very well and the correct answer was obvious from the choices:

Screen Shot 2018-08-19 at 9.05.42 AM.png

Despite not liking the question so much for a calculus exam, I thought it would make a pretty neat estimation problem for kids. My older son was looking at exponentials and logarithms this week anyway, so using this question as an estimation problem sort of fit in naturally with what he was doing anyway this week.

I started off today’s project by introducing the problem and asking the kids how they would approach it.

My younger son had a bit of a difficult time understanding the problem – which wasn’t a big surprise. My older son wanted to start by estimating what the square root of e was. Not the starting idea I was expecting, but it made for a good estimating problem:

Now that we we’d guessed that e^{x/2} would look a lot like 1.65^x we decided to draw the region.

My younger son thought that the region would be a trapezoid – my older son thought it would be more of a curved shape.

Now that we had the shape drawn, we could estimate the area. We actually used the idea that it was nearly a quadrilateral to make that estimate.

Finally, we used our estimate of the area (3.71 square units) to see if we could identify the correct answer from the choices given in the original problem:

Walking through the proof that e is irrational with a kid

My son is finishing up a chapter on exponentials and logs in the book he was working through this summer. The book had a big focus on e in this chapter, so I thought it would be fun to show him the proof that e is irrational.

I started by introducing the problem and then with a proof by contradiction example that he already knows -> the square root of 2 is irrational:

Now we started down the path of proving that e is irrational.  We again assumed that it was rational and then looked to find a contradiction.

The general idea in the proof is to find an expression that is an integer if e is irrational, but can’t be an integer due to the definition of e.

In this part we find the expression that is forced to be an integer if e is irrational.

Now we looked at the same expression that we studied in the previous video and showed that it cannot be an integer.

I think my favorite part of this video is my son not remembering the formula for the sum of an infinite geometric series, but then saying that he thinks he can derive it.

This is a really challenging proof for a kid, I think, but I’m glad that my son was able to struggle through it. After we finished I showed him that some rational expressions approximating e did indeed satisfy the inequality that we derived in the proof.

More calculus ideas for kids inspired by Grant Sanderson

I’m enjoying thinking about how to share Grant Sanderon’s latest calculus video series with kids. My goal is not remotely to develop a calculus course, but just to give kids an opportunity to see and explore some of the basic ideas that Sanderson shares in his video series. At a high level, things like slope of the graph of a function are easily accessible to kids even if the calculations required to make the ideas precise might be beyond them. Our projects so far are here:

Sharing Grant Sanderson’s Calculus ideas video with kids

Sharing Grant Sanderson’s “derivative paradox” video with kids is really fun

Sharing Grant Sanderson’s derivative paradox video with kids part 2

Sharing Grant Sanderson’s “derivatives through geometry” video with kids

So, walking the dog tonight I came up with two ideas for discussion:

(i) How does the length of the hypotenuse of a right triangle change as the length of one of the sides changes?

(ii) If a function has the property that the slope of the tangent line is the same as the value of the function, what would that function look like?

We began with a quick review / discussion of slope in the context of a curve. This concept is still new to the boys and I wanted to have one quick review before we dove into the main project:

Next we moved on to the right triangle problem – how would the length of the hypotenuse change when one of the side lengths changed? The boys were able to grasp some basic ideas around when the changing side was short (near zero length) and very long (near infinite length), and we were able to make a sketch of what the derivative might look like just from these basic observations:

The next project was a basic (the most basic?) differential equation -> a function has the property that the derivative at a point is equal to the value of the function at that point. The value of the function at 0 is 1. What does this function look like?

Finally, we went up to the computer to use Mathematica to explore our two questions. For purposes of this higher level conceptual overview, it is nice that Mathematica’s built in functions allow us to study these two questions without having to do the calculations ourselves:

The more of these project I do, the more I’m convinced that this is a useful exercise for kids. For now at least, I can’t think of any reason why learning about these basic ideas at the same time you are learning about functions will cause problems.

Never tell me the odds – talking math and Powerball

We did a little impromptu talk about the math behind Powerball this morning. We also did a similar talk last summer:

Playing around with the odds of winning Powerball

but I learned this morning that the game has changed slightly since our original talk, so it seemed worthwhile revisiting the topic of Powerball odds today.

The official listing of the odds for each prize in Powerball is here:

The official odds of winning various prizes in Powerball

Screen Shot 2016-01-10 at 8.36.20 AM

The specific topics for today were:

(1) What is the probability of winning the grand prize?

(2) What is the probability of getting only the Powerball correct?

(3) Since the chance of getting winning the grand prize is about 1 in 292 million, what is the probability that no one will win if 292 million people pick numbers at random?

The third part was a little hard for the kids to understand than I was expecting it to be, but the extra time we spent talking about this question made the project worthwhile.

Here’s the first part – the chance of winning the grand prize:

 

The next part was about the chance of getting only the Powerball correct. The FAQ on the Powerball site has a funny comment about this particular prize.

 

Finally, the talk about no one winning if 292 numbers were guessed took three parts. Here’s the introduction to that question. The kids were a little confused about how to approach it.

 

I tried to simplify the problem by looking at a case where 2 people guess at a number that is either 0 or 1:

 

After looking at the easier version of the problem we returned to the problem of no one winning the grand prize in Powerball if 292 million people played. It was sill difficult for my younger son to understand this problem, but we did eventually get to the punchline – the probability is approximately 1 / e.

Where did e come from??

 

So, a fun project. I’m guessing there will be a lot of conversations about Powerball over the next few days – maybe that’ll get kids interested in talking about the math behind the game, too.

Frank Farris’s patterns

A couple of weeks ago Evelyn Lamb’s article Impossible Wallpaper and Mystery Curves introduced me to Frank Farris’s work. On Saturday I stumbled on his book at Barnes and Noble:

  

I was excited to try out some of his ideas with the boys even though they use complex numbers and exponentials which are over their heads. We did the whole exploration this morning using Mathematica.

To start, we just explored the exponential function.

Next we moved to looking at sums of two exponential functions. The boys were surprised by the graphs and we played around with a few more examples. They had some interesting ideas about what the pictures looked like, and I’m glad that the pictures also reminded them a little of Anna Weltman’s loop-de-loops.

Next we moved on to sums of three exponential functions motivated by the idea of trying to produce another kink in the loop. There was a little discussion at the beginning of this part of the talk about complex variables. I thought going down this path was going to be too difficult to explain, so I tried to bring the conversation back to the sums. I love the ideas they had about symmetry here.

Next we looked at Farris’s “mystery” shape and played around a bit more with the ideas. These shapes also led to fun conversations about symmetry:

Finally, I let the kids just play around. As I was writing up this project I got a “hey dad, come here and look at this cool shape” call:

  

So, despite the math underlying these shapes being a little over their heads, the kids seemed to really enjoy seeing these shapes. I loved hearing their ideas and I loved seeing them play around with the ideas for a long time after we turned off the camera.

Also, Farris’s book is absolutely amazing – you’ll love the ideas and the presentation, and probably most of all the incredible pictures he creates from the ideas!

Michael Pershan’s Exponential post (part 2 /3 )

Despite an extra day to try to think things through I remain confused about my own approach to teaching / talking about exponential functions.   I’m actually struggling to even understand what the struggle is.  After all, running across this fun little connection between 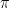\pi and e as a college freshman is what convinced me to major in math:

Formula

As I mentioned in the first post in this series, my approach to teaching exponentials has not been nearly as formal as my approach to teaching arithmetic.  We began by talking about powers where I introduced exponents as essentially a time saver.  Probably like just about everyone who has ever talked about exponents,  one of the early conversations was about the zeroth power and negative powers.  That talk about exponents with my younger son remains one of my favorite math  conversations he and I have ever had:

Feels as though you are almost forced to introduce integer exponents early one if you want to talk about place value or different bases or other similar topics, but the path to exponentials from here just isn’t that satisfying to me.  You’ll have to introduce fractional powers and then define non-rational powers by some sort of limit process (at least if you want to approach things formally).  If you are going to bed at night fearing a Grant Wiggins-like “conceptual understanding of exponential functions” exam, you probably won’t like this path at all.

There are fun topics, though, so I’m not suggesting that integer or rational exponents are a waste of time.  Two of my favorite topics here have been finding a formula for the Fibonacci numbers while we were studying quadratic equations:

https://mikesmathpage.wordpress.com/2014/02/07/the-quadratic-formula-and-fibonacci-numbers/

and talking about Graham’s number, which is one of the most fun math activities that we’ve ever done, and probably as much fun and excitement with integer powers as you are ever going to have.  It took me a week to figure out how to put this one together (and I stopped after a week, because there was no way I was going to figure out how to do it anyway!)

https://mikesmathpage.wordpress.com/2014/04/12/an-attempt-to-explain-grahams-number-to-kids/

With all this background I’m kind of surprised that I can’t really think of a nice, easy transition from exponents to exponential functions.   As I was riding home last night I tried to keep a look out for anything I saw that I naturally thought of as being associated with an exponential function – something / anything that kids might see occasionally in their life.  I couldn’t find a single thing which made me a little sad.  Maybe I’m just not being creative enough.

In yesterday’s post I mentioned a few things from finance and probability where exponential functions appear pretty naturally, but those are well outside the realm of things that kids see or worry about.   What I didn’t mention was a different field where exponentials play an incredibly important role – physics.  Representing waves in the form e^{i * \omega t} is pretty convenient, to say the least, but again is way outside of what might be reasonable examples for kids.

So, I’m lost.  A non-formal approach starting with integer exponents does let you talk about some really interesting problems, but doesn’t really seem to set you up too well to move to exponential functions in general.  I’m a little frustrated at my inability to find  any great (or even reasonable) natural exponential examples to share with kids.  And, to top it all off,  starting with a formal approach like defining 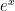e^x as the limit as n approaches infinity of 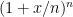(1 + x/n)^n just seems stupid.

The perplexing thing is that both 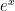e^x and ln(x) play such incredibly important roles in math.  You’d think that there would at least be a few easy examples you could talk through with kids to introduce / motivate these ideas.  I mentioned in yesterday’s post that I gave one formal approach a try.    That was in response to a question I saw about logs on twitter when I happened to be talking about them with my older son.  That question motivated me to throw together a fun overview of some of the areas in math where logs are part of important results.  I wasn’t expecting my son to get much of anything out of it other than to see some really amazing math involving prime numbers.  That blog post is here:

https://mikesmathpage.wordpress.com/2014/04/16/a-little-non-standard-fun-wiht-logs/

Tomorrow, or over the weekend, I’ll try to come out of the fog and write about what I’d like my kids to learn about logs and exponentials.  Hopefully I’ll have it all figured out by then.  Ha!