Tag: Geometry Revisited

Sharing Stewart’s theorem with my son

My older son had a problem about finding the length of an angle bisector in a 3-4-5 triangle in his enrichment math class last week. Solving this problem is a little tedious, but also gives a great opportunity to introduce Stewart’s theorem. I first learned about Stewart’s theorem from Geometry Revisited when I was in high school. Here’s an explanation of the theorem on Wikipedia:

Stewart’s theorem on Wikipedia

I started off the project tonight by reviewing the original problem with my son:

Next I briefly introduced the theorem and then we got interrupted by someone knocking on our front door:

Now I showed how the proof goes. We had a brief discussion / reminder about the relationship between \cos(\theta) and \cos( 180 - \theta ) and after that the proof went pretty quickly:

Finally, we returned to our original triangle to compute the length of the angle bisector using Stewart’s Theorem. The computation is still a little long, but now the calculations themselves are pretty straightforward:

Definitely a beautiful theorem. It is amazing that the law of cosines simplifies so nicely and that computing the lengths of cevians of a triangle.

Varignon’s Theorem

Yesterday Patrick Honner posted a nice illustration of Varignon’s Theorem by one of his students:

It is particularly fun to move the points around to form a non-convex quadrilateral and see that the midpoints still form a parallelogram.

As with many advanced concepts in geometry, my introduction to Varignon’s theorem came from Geometry Revisited by Coxeter and Greitzer. I remember the theorem partially because of the lovely introductory statement in the book:

“The following theorem is so simple that one is surprised to find its date of publication to be as late as 1731. It is due to Pierre Varignon (1654 – 1722).

Theorem 3.11. The figure formed when the midpoints of the sides of a quadrangle are joined in order is a parallelogram, and its area is half that of the quadrangle.”

The chapter also presents three other wonderful theorems and some super problems including this one:

“1. [Show that] the perimeter of the Varignon parallelogram equals the sum of the diagonals of the original quadrangle.”

So, this special parallelogram has some really interesting properties!

As a fun follow up this morning, my older son was working on some problems from the 2006 AMC 8. Looking over the test I noticed that problem #5 was a simple example of Varignon’s theorem:

Problem #5 from the 2006 AMC 8

I chose a different problem to go through with my older son, but thought my younger son would like this one. It was a challenge, but he eventually was able to work through it. It is kind of fun to think of this basic problem as one that opens the door to this beautiful theorem.

 

Cathy O’Neil on Trig

Cathy O’Neil published this awesome piece about trig on her blog yesterday:

Fuck Trigonometry

It created quite a conversation. Yay!

Her husband’s comment at the end of the post caught my attention and I spent most of yesterday sort of daydreaming about his point:

When I mentioned my hatred of trigonometry to my husband, he countered with an argument that wasn’t mentioned so far. Namely, that we have really no reason to teach high school kids any given thing, so we just choose a bunch of things kind of at random. Moreover, he suggested, if we remove trig, then meeting people at an airport would just elicit some other reason for hating math. We’d be simply replacing trig with some other crappy topic choice.

I think I’m leaning towards agreeing with him. I’m certainly not sure I could make a convincing argument about why trig *needs* to be taught. In fact, with 3D printing and maybe even Zometool sets becoming cheaper and easier to find, my vote would probably be to try more fun geometry projects before diving into trig. Our Gosper curve project, for example, is something that I think kids would find more entertaining that trig identities:

Exploring the Gosper Curve

The passion in the conversation around Cathy’s post also surprised me a little – I didn’t realize that so many people had such strong feelings about trig! Most of the internet math flame wars I see are about addition or fractions – watching people fight about trig was so refreshing 🙂

Thinking back to my high school trig class with Mrs. Kovaric yesterday I honestly couldn’t remember really having any strong feelings one way or another. Without any strong opinions to fight about (ha ha) I started thinking about some fun math ideas related to trig that I’d learned either in high school or in college. Not reasons to teach trig, for sure, but definitely more fun than memorizing identities!

(1) The Extended law of Sines

One idea everyone sees in trig class is the law of sines – in any triangle ABC, A / Sin(A) = B / Sin(B) = C / Sin(C). Pretty neat relationship, but if these three expressions are all equal to each other is their value special? Turns out that it is:

 

(2) Stewart’s theorem

This is a cool theorem which gives the length of a line segment from a vertex of a triangle to the opposite side. As with the extended law of sines, this theorem is something that I found in Geometry Revisited in high school. The proof (that I know) involves the law of cosines:

Trig

Also, the law of cosines came up in a surprising way in an introductory geometry talk I had with my older son this past school year. This conversation was an unexpected (to me) way that you could talk about the ideas behind the law of cosines in geometry class:

When we accidentally derived the law of cosines

(3) The sum of the inverse squares

Using the Taylor series for Sin(x) and the fact that the roots are integer multiples of 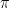\pi, you can prove that:

1 + \frac{1}{4} + \frac{1}{9} + \ldots + \frac{1}{n^2} + \ldots = \frac{\pi^2}{6}

It was incredibly cool to learn that there was a known formula for all of the inverse even powers (solved by Euler in the 1700s, if I remember right), but that a closed form for the odd powers greater than 1 was not known. This is a neat example of an unsolved math problem that high school students can understand and even play around with a little. I’ve always hoped to see a closed form solution for the sum of the inverse cubes.

Another fairly famous trig-related sum problem that blew me away in high school is this incredible sum:

Let 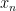x_n be the 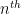n^{th} positive solution to the equation 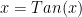x = Tan(x). Find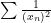 \sum \frac{1}{(x_{n})^{2}}

The particularly amazing thing about this problem is that you can find the sum even though you can’t write down a closed form for any of the expressions that are in the sum!

(4) A surprising integral

I went to college planning on majoring in aerospace engineering – that’s what you do with math, right 🙂

Sitting in an introduction to complex analysis class my freshman year, I ran across this interesting little problem:

Formula

Seeing this problem made me want to major in math rather than engineering – it was absolutely amazing to me that 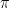\pi and e could be connected in such a seemingly mysterious way.

(5) Circles on a sphere

This one is the one and only time that I’ve used trig directly at work (probably more than 10 years ago, though I don’t remember the exact timing).

One of the guys in our office who thinks about hurricane insurance had a list which gave the latitude and longitude of the center of every hurricane that hit North America for the last 50 or so years. The list had coordinates for the center in time increments of 6 hours. The question he wanted to answer was relatively simple: given a specific latitude / longitude (say Miami or New York City, or something) how many Hurricanes had come within a given distance of that city (50 miles, 100 miles, . . . .).

He’d tried to write a really quick and back of the envelope program to answer this question but it was giving answers that seemed really wrong. To calculate distance correctly you need a little bit of trig because you have to factor in how far north you are. Adjusting the distance formula for a given latitude helped him get to the right answer. There were a few other little math-related tricks in the program, too, such as checking whether or not the path between two points came within the desired distance even if the endpoints were outside of the distance. Without trig, the distance calculations in this project were easy to get wrong.

Anyway, not a list of reasons to teach trig, but rather just a few fun trig-related things that Cathy’s post got me thinking about. Hopefully slightly more fun than memorizing identities 🙂

Although if you’ve made it this far and do like trig identities, though, a recent Terry Tao post should be right up your alley:

A “cute” differentiation identity

Power of a point and some fun equalities

Way back in 2011 when I first started thinking about doing math movies I filmed a set of practice lectures based on the first couple of sections of Geometry Revisited. The main point was to evaluate myself talking about math – at that point it had been more than 10 years since I’d been in a classroom. Thefirst practice lecture where I try to shake of some of the old rust was about the extended law of sines.

What I learned in my trig class back in high school was that for a triangle: a / Sin(A) = b / Sin(B) = c / Sin(c). That’s an incredible identity, but there’s a pretty natural question that I never thought to ask – if these expressions all have the same value, is there something special about that value? That’s the question that this lecture tries to answer:

Today I went through a similar exercise with my son as we worked through the review section in the Power of Point chapter in our geometry book. Studying the power of a point identities you learn that lots of products involving lines and circles are equal to each other – but does the value of the product have any special significance? Let see . . . .

So, for points outside for the circle we just found the value of the products that come up in the power of a point formulas. We saw, though, that when the point is inside of the circle we’ll need to have a different formula. We derive that companion formula here:

So, a fun trip down memory lane for me this morning while reviewing some power of a point ideas. Hopefully work like this plants a little mathematical idea in my son’s mind – it two (or more) expressions are equal to each other, maybe there’s something special about the value of those expressions.

Ceva’s Theorem – a neat example of ratios in geoemtry

This morning my older son and I worked through a great example problem in Art of Problem Solving’s Introduction to Geometry book.  By amazing luck the section is one of the sections that Art of Problem Solving highlights on their web page about the book, so feel free to check out problem 5.7 here (and don’t peek at the solution!):

Click to access exc1.pdf

We actually came across the problem yesterday, but I wanted to devote an entire day to it today because the clever use of ratios in this problem is so instructive.  I definitely didn’t want the mathematical beauty in this example to be lost because we had to rush through it.  Also, we’ve been away from fractions and ratios for a while so my guess was that it would take a full hour to go through the problem in detail.  It did.

In the middle of talking through the problem this morning I remembered that the proof of Ceva’s theorem also uses ratios in a clever way, and thought a fun follow up on the example from this morning would be walking through the proof of Ceva’s theorem tonight.  It really is amazing that you can prove this beautiful theorem with just the area formula for triangles and a clever use of ratios.

In the presentation below, I’m following the proof given in section 1.2 of Geometry Revisited, which is where I learned about the theorem back in high school (and since I was too lazy to take a new picture, check out C.D. Olds’s Continued Fractions book too!!):

Book 2

I started with the statement of the problem and showed how to get started on the proof by making some simple observations about areas of triangles.  Then we began looking at the neat ratio idea:

Since this idea about ratios really isn’t that intuitive I wanted to take a little break from the geometry to just get a better understanding of why ratios behave in this seemingly strange way.  My son had the nice idea to look at the relationship abstractly to see why it was true.  It is a little funny that the relationship is easier to see abstractly than with specific numbers.

In the last part of the proof we show that the product of the three ratios is equal to one.  In the first video we showed that the first ratio we were looking at was equal to the ratio of the areas of two triangles.  We apply the same argument for the remaining two ratios and find two other sets of triangles whose areas are in the ratio that we were looking at originally.

If you are careful with how you label these triangles (and I wasn’t) you see quickly that the product of the three ratios is equal to one.  If you aren’t careful it takes a little bit of extra time to see that all of the products cancel.

So, a really fun example.  To a kid learning geometry it probably seems pretty surprising that a concept from arithmetic is going to lead to such an impressive result in geometry.  I like that aspect of showing this proof, too, and I also like the reverse – namely that a day of studying geometry gave us a great chance to review ratios.

A super fun day overall, and all from one cool example from our Geometry book!

Mr. Honner does it again

Patrick Honner has several blog articles about poor problems (sometimes outright mistakes) on some of the exams that New York state requires for students. Since I don’t live in NY I’m not super familiar with these exams, though Mr. Honner’s posts actually make me happy that I’m not. I get the feeling that the more I knew about them the more they’d drive me crazy.

In any case, his latest article is here:

Regents Recap — June 2014: When Good Math Becomes Bad Tests

and the problem he discusses is:

“The medians of a triangle intersect at a point. Which measurements could represent the segments of one of the medians?

(a) 2 and 3

(b) 3 and 6

(c) 3 and 4.5

(d) 3 and 9”

Unlike some of the prior problems that he has written about the problem itself doesn’t have any mathematical flaws. Instead this problem is simply testing if you know a single math fact. Really no deep understanding of geometry is required to solve it at all if you know this fact. I think that Mr. Honner’s concern – which is essentially that if state exam questions end up looking similar to this one, math education is just going to turn into something equivalent to prepping for a night on Jeopardy – is spot on.

This critique hit me for another reason, though. Three years ago when I decided that I wanted to start making fun little math videos for kids, I thought that I should practice a little and see if I actually had any ability to explain math. At that point it had been more than 10 years since I’d been in front of a classroom. Oh, and 10 years in finance doesn’t exactly sharpen your explanation skills.

What I decided to do was grab my copy of Geometry Revisited off the shelf and pretend I was doing a few lectures from the book. I went through the first two chapters or so, but two of the early sections are relevant here. The second “lecture” was about Ceva’s theorem, which is a beautiful theorem with a fascinating and incredibly instructive proof (keep in mind that I’d not talked about math for a long time in this video, so it isn’t the best. Also my older son is watching for some reason I don’t remember):

So we get a beautiful theorem with a really instructive proof right in the second section of Geometry Revisited! Also, I saw that Steve Leinwand gave a lecture at a conference for teachers last week and said that ratios were one of the most important pieces of early math. Ratios play a surprising role in this proof of Ceva’s theorem, so it may have even more educational value than I realized the first time around. Finally, the result we can see pretty easily from Ceva’s theorem that is relevant to the question on the NY state exam is that the medians of a triangle intersect in a single point.

With a few fun ideas about cevians in hand, you might be interested in learning even more, and Geometry Revisited doesn’t disappoint. The next section shows a couple of nice results about the medians that also have incredibly instructive proofs (the part about the medians starts at 3:20):

I remember vividly how going through these early sections in Geometry Revisited reminded me how much I loved math. With just two short sections on Ceva’s theorem and medians we have a couple of beautiful results and several really instructive proofs for students to see. I understand that no all kids are going to find these ideas to be as fascinating as I do, but I think that lots of kids will. It seems like such a shame to me to reduce it all to the question posed above, and frankly even worse to essentially reduce it all to something like –

Answer: They trisect each other.

Question: What do the medians in a triangle do?