Revisiting Grant Sanderson’s “fair division” video thanks to an Amy Hogan tweet

I saw a tweet from Amy Hogan this morning that reminded me of an old project:

Two thieves steal a necklace w/ 10 rubies and 14 emeralds, fixed in some arbitrary order on a loop of golden string. Show they can cut the necklace in 2 places so when each thief takes one of the resulting pieces, they get ½ the rubies and ½ the emeralds. From @MoMath1 #mathchat

— Amy Hogan (@alittlestats) June 6, 2021

The old project is here:

Grant Sanderson’s “Fair Division” video shows a great math project for kids

And Grant’s video is here:

Before we started the project today, I had my son watch Grant’s video. Here are some of his takeaways:

Now we tried to see if we could find a fair division of a string with two colors using only two cuts:

Finally, to wrap up we tried to see if we could do a fair division of a string with three colors using three cuts:

This is a fun and relatively easy project for kids, and also a way for them to see some really fascinating advanced math!

Sharing Grant Sanderson’s Hamming Code video with my younger son

Yesterday Grant Sanderson published a fantastic set of videos on Hamming codes. I watched the first one with my younger son last night:

Today we talked about some of the ideas in the video – starting with some of the things he thought were interesting:

Next I had him work through one of the examples in Grant’s video – I didn’t realize it was an example of an error since I just pulled it off of a screen shot, but we discovered the error talking through the example:

Finally, we went back to the same example. This might seem like a strange thing to do, but Grant’s example had an error in the parity bit and I wanted to make sure my son understood that the error correcting codes could also detect that kind of error.

I love Grant’s work – it makes for such a fun and easy way to explore ideas that kids wouldn’t normally see in their school math.

Sharing Grant Sanderson’s “Simulating an epidemic” video with my kids

Last week Grant Sanderson published a fantastic video showing some simple models of how a virus can spread through a population.

All of the common pandemic models are pretty complex and have tremendous uncertainty in their parameters, but Grant’s video does an incredible job of showing their strengths and weaknesses.

Today I watched the video again, but this time with my kids. I asked them to take some notes and then we talked about what they thought was interesting. It is always fascinating to hear what kids take away from math / science content.

Here’s what my younger son (in 8th grade) had to say:

Here’s what my older son (in 10th grade) had to say:

Sharing Grant Sanderson’s “Surface Area of a Sphere” video with my older son

Last week Grant Sanderson published an incredible video about the surface area of a sphere:

By happy coincidence my older son is spending a little time reviewing polar coordinates now. Although not exactly the same ideas, I think there’s enough overlap to make studying Sanderson’s new video worthwhile.

So, I’m going to do a 6-part project going through the video. Tonight we watched it and my son’s initial thoughts are below. Each of the next 5 parts will be spent discussing and answering the 5 questions that Sanderson asks in the 2nd half of the video.

Here’s question #1:

We’ve been away from right triangle trig a little bit lately, so I was interested to see how my son would approach this problem. His approach was a bit of a surprise, but it did get him to the right answer:

The next question in Grant’s video is about how the area of one of the rings on the sphere changes when you project it down to the “base” of the sphere (see the picture above).

I thought that answering this question would be a really good geometry, trig, and Calculus exercise for my son:

Now we get to a really interesting part -> Question #3

Grant asks you to relate the area you found in question 2 – the area of a ring around the sphere projected down to the center of the sphere – to the area of a different ring around the sphere.

Here’s my son’s work on this problem:

Finally – my son answers questions #4 and #5 after a quick review of the previous results. He was a little tired tonight, but we needed to squeeze in these two questions tonight because I have to travel for work tomorrow.

Here’s question #4:

and #5:

And here’s his work on those two questions:

A fun experiment sharing Grant Sanderson’s Topology video with a kid

I saw a really neat new video from Grant Sanderson this morning:

We’ve actually looked at the ideas Grant is sharing here before, but my son didn’t remember:

Grant Sanderson’s “Fair Division” video shows a great math project for kids

For today I asked my younger son (in 7th grade) to watch the video and take some notes. After he finished we started taking about what he saw. He was interested in the Borsuk–Ulam theorem and also he thought the “stolen necklace problem” was pretty neat:

Next we talked about the proof of the Borsuk-Ulam theorem. I was really happy that most of the main ideas that Grant shared in his video stuck in my son’s mind.

We wrapped up by talking about the “stolen necklace” problem. We did a few examples about that problem and then had a fun discussion about the equation for a sphere. My son was curious about the difference between the boundary of the sphere and the all of the points inside the sphere. In particular, he was wondering why the equation for a sphere Grant used was and not

From there we had an interesting discussion about dimension. I didn’t expect the conversation to go in that direction, but I guess you never know what a kid is going to take away from a video about some pretty advanced math ideas 🙂

Working through Calculus with my older son

This year my older son wanted to learn calculus. I was hesitant, but we’ve finished the Art of Problem Solving books and also have done (as of September 2018) about 850 stand alone math projects, so I couldn’t find a good reason to object.

The collection of calculus books I had from 20 years ago seems to have dwindled down to just 2 -> a 3rd edition of Stewart’s Calculus, and the book by Spivak. Spivak feels too hard for an introductory course, so I chose Stewart.

Last week we worked through the chapter on limits and continuity, and this week we are starting the section about derivatives. I’ve also been using Grant Sanderson’s fantastic video series “Essence of Calculus” and used the 3rd video in that series to introduce some ideas about derivatives last night. Here’s that video:

Before diving into Stewart’s chapter on derivatives, I reviewed the ideas and challenges in Sanderson’s video this morning. Here’s the conversation about the derivative of $f(x) = x^2$

The main idea I want to be sure that he understands is that small changes in functions as the input changes can be represented as:

Next we worked through 2 of the challenges that Sanderson gave in his video.  The first is to use a geometric argument to find the derivative of .

The second challenge in Sanderson’s video is a bit more challenging -> Use a geometric argument to find the derivative of .  I helped out here a bit more because the arguments are bit more subtle, but he was able to find the right argument.

I’m hoping to be able to write about our calculus conversations once or twice a week starting with today’s conversation. Hopefully this will be an exciting year studying calculus.

Using Grant Sanderson’s Pythagorean Triple video for an introductory trig lesson

My older son is starting to learn trig and I wanted to show him the surprising connection between the exponential function and trig functions. Grant Sanderson’s video on Pythagorean triples from earlier this year came to mind:

After my son watched the video tonight I asked him to talk about some of the ideas. Here’s what he had to say – I was happy that many of the ideas that Sanderson presented sank in:

Now I showed him the incredible formula = Cos(x) + i*Sin(x). Although I just present the formula, the complex number ideas after that are exactly the same ideas that are in Sanderson’s video:

Now I showed him how this formula makes some of the standard trig identities really easy to both derive and remember. The ideas here were really the inspiration for the video because he asked me this morning if the trig functions were linear.

We specifically looked at formulas for Cos(2x) and Sin(2x) here.

Now we used the formulas in a couple of simple examples. First we looked at 45 degrees, then 30 degrees, and then we looked at the angles in a 3-4-5 triangle:

This project was a fun way to introduce an amazing idea in math and also hopefully a nice way to show my son that ideas in trig go way beyond triangles.

Sharing Grant Sanderson’s “Pi and Primes” video with kids part 2:

Grant Sanderson’s latest video explaining a connection between pi and prime numbers is absolutely fantastic:

This video is sort of at the edge of what kids can understand, but it was fun to explore a few of the ideas with them even if understanding 100% of the video was probably not realistic. Our project on the first 10 min of the video is here:

Sharing Grant Sanderson’s Pi and Primes video with kids part 1

Also, we did a project on a different approach to the problem Sanderson is studying previously:

A really neat problem that Gauss Solved

I intended to divide our study of Sanderson’s video into three 10 minute sections, but the second 20 minutes was so compelling that we just watched it all the way through. After watching the last 20 min a 2nd time this morning I asked the kids what they found interesting. The three topics that they brought up were:

(i) The function,

(ii) The formula for , and

(iii) Factoring ideas in the Gaussian integers

Following the introduction, we talked about the three topics. The first was factoring in the Gaussian integers. We talked about this topic in yesterday’s project, too.

Next we talked about the function. I had no idea how the discussion here was going to go, actually, but it turned out to be fantastic. The boys thought the function looked a lot like “remainder mod 4”. Why it does look like that and why it doesn’t look like that is a really neat conversation with kids.

Finally we talked through the formula that Sanderson explained for It probably goes without saying that Sanderson’s explanation is better than what we did here, but it was nice to hear what the boys remembered from seeing Sanderson’s video twice.

I love having the opportunity to share advanced math with kids. I don’t really have any background in number theory and probably wouldn’t have tackled this project with out Sanderson’s video to show me the path forward. It really is amazing what resources are on line these days!

Sharing Grant Sanderson’s “Pi and Primes” video with kids. Part 1

[This one was written up pretty quickly because we had to get out the door for some weekend activities. Sorry for publishing the un-edited version]

Grant Sanderson has a new (and, as usual, incredible) video on “Pi hiding in prime regularities”:

By coincidence, we’ve done a project on this topic before:

A really neat problem that Gauss Solved

The old project is based on Chapter 8 from this book:

Sanderson’s new video is pretty deep and about 30 min long, so I’m going to break our project on his video into 3 pieces. Today we watched (roughly) the first 10 min of the video. Here’s what the boys took away from those 10 min:

The first topic we tackled today was how to write integers as the sum of two squares. This topic is the starting point in Sanderson’s video and the main point of the project from the Ingenuity in Mathematics project. We explored a few simple examples and, at the end, talked about why integers of the form 4n + 3 cannot be written as the sum of two squares:

Next we turned our attention to the complex numbers and how they came into play in (the first 10 min of) Sanderson’s video. My focus was on the Gaussian Integers. In this part of the project we talked about (i) why it makes sense to think of these as integers, and (ii) how we get some new prime numbers (and also lose a few) when we expand our definition of integers to include the Gaussian Integers:

To wrap up I mentioned the topic from the prior project. The question there is something like this -> since counting the exact number of ways an integer can be written as the sum of two squares is tricky, can we say anything about how to write an integer as the some of two squares?

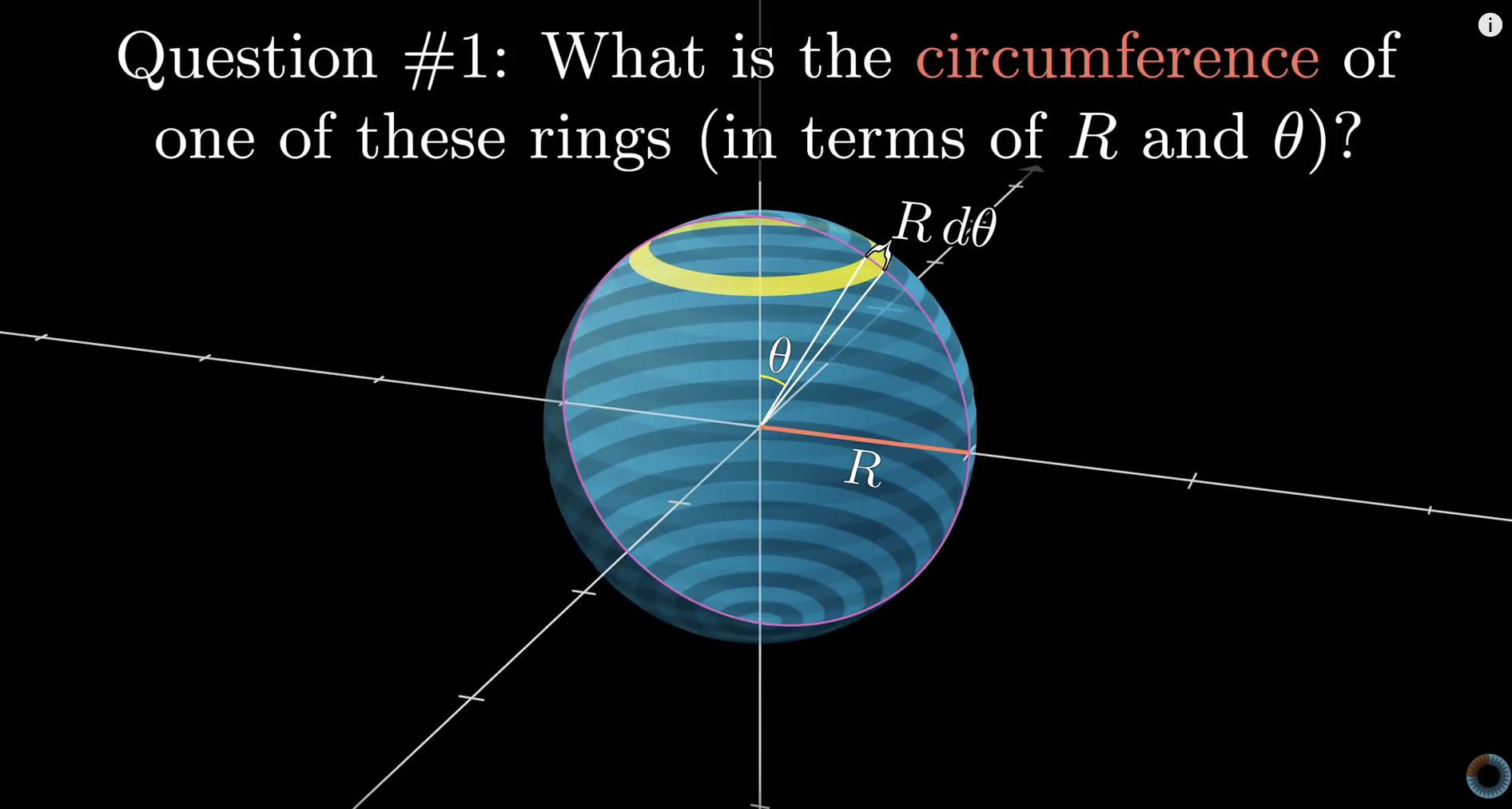
Turns out you can, and that the average number of different ways to write a number as the sum of two squares is 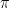. Pretty incredible.

[and, of course, I confused an and 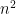in the video 😦 Looking at the prior project will hopefully give a better explanation than I did here . . . . ]

I’m always excited to go through Grant Sanderson’s video with the boys. He has an amazing ability to take advanced ideas and make them accessible to a wide audience. Sometimes making the topic accessible to kids requires a bit more work – but Sanderson’s videos are a great starting point.

A fun calculus problem for kids – playing with derivatives and absolute value

I’ve been doing a few “calculus for kids” projects after seeing Grant Sanderson’s essence of calculus series. The series made me see that some of the high level ideas are completely accessible to kids and it has been fun to explore some of those concepts.

Today I thought it would be fun to see what they thought the derivative of absolute value would look like – they had some neat ideas:

Next I thought I would turn the problem around – what if absolute value was the derivative! What would the function look like. This problem was much more challenging. In the first video they spent most of the time just getting their head around the problem:

So, now that they had the ideas in place to solve the problem, they started drawing pictures. The process of getting to the correct graph was really interesting to watch:

The more I think about this calculus project, the more fun I think it is going to be. Many of the ideas in Sanderson’s series will be out of their reach, but some of the high level concepts are incredibly fun to share with kids.