Yesterday we were listening to Patrick Honner’s appearance on the My Favorite Theorem podcast. Honner was discussing Varignon’s Theorem. We actually have discussed this appearance before, but the kids hadn’t listened to the podcast, yet:
Sharing Patrick Honner’s My Favorite Theorem appearance with kids
After listening to the podcast I asked my older son what his favorite theorem was:
However, after giving up on the idea initially (!) I looked at the Wikipedia page for the Banach-Tarski paradox and found an idea that I thought might work. Here’s the page:
Wikipedia’s page on the Banach-Tarski paradox
The idea was to share the first step in the proof – exploring the Cayley graph of 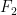 – with kids. Here’s the picture from Wikipedia:
– with kids. Here’s the picture from Wikipedia:

So, here’s what I did.
First I introduced the boys to some basic ideas about a free group on two generators. I used a Rubik’s cube to both demonstrate the ideas and to show why a Rubik’s cube didn’t quite work for a perfect demonstration (I know that part of the video drags on a bit, but stay with it – there is a nice surprise):
Next we talked about the free group with two generators in more detail. My younger son accidentally came up with a fantastic example that helped clarify how this free group worked.
Then there was a bit of a surprise misconception that I only uncovered by accident. That led to another important clarification.
So, completely by accident, we had a great conversation here.
In the last video they boys thought you could use the “letters”  only once. In the beginning of this video I clarified the rules.
only once. In the beginning of this video I clarified the rules.
Next we began to talk about the representation of our free group by the Cayley graph from Wikipedia pictured above. I was really fun to hear how the boys described what they saw in this graph.
Finally, we looked at two different ways to break the Cayley graph into pieces. This video is a little long, but it has a simplified version of the main idea in the Banach-Tarski paradox.
The first decomposition of the Cayley graph is into 5 pieces -> the identity element, words that start with  , words that start with
, words that start with  , words that start with
, words that start with 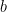 , and words that start with
, and words that start with  . This decomposition is pretty easy to see in the picture.
. This decomposition is pretty easy to see in the picture.
The second – and very surprising decomposition is as follows:
The combination of (i) the words that start with  and (ii)
and (ii)  multiplying (on the left) all the words that start with
multiplying (on the left) all the words that start with  gives the entire set. The same is true for the combination of (i) the words that start with
gives the entire set. The same is true for the combination of (i) the words that start with 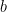 and (ii)
and (ii) 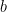 multiplying (on the left) all the words that start with
multiplying (on the left) all the words that start with 
Although the words describing this decomposition might not make sense right away, you’ll see that the boys had a few questions about what was going on and eventually were able to see how this second decomposition worked.
And this second decomposition gives a huge surprise -> we’ve taken 4 subsets, combined them in pairs and created two exact copies of the original set. Ta da 🙂
This project is an incredibly fun one to share with kids. I’m pretty surprised that *any* ideas related to the Banach-Tarski paradox are accessible to kids, but the simple ideas about the Cayley graph of 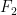 really are. Using those ideas you can show the main idea behind the sphere paradox without having to dive all the way into rotation groups which I think are a little more abstract and harder to understand.
really are. Using those ideas you can show the main idea behind the sphere paradox without having to dive all the way into rotation groups which I think are a little more abstract and harder to understand.
Anyway, this one was a blast!











