An AMC 10 problem with some neat lessons about a 15-75-90 right triangle

This problem (#22 from the 2014 AMC 10a) gave my son some trouble this morning:

We ended up having a nice talk about the problem this morning. To see if the ideas really sunk in, I asked him to talk through the solution tonight, and he did a nice job:

After we finished, I wanted to go back to the 2014 AMC 10 and just happened to notice that google was also showing that Art of Problem Solving had a video about the problem. So, I thought it would be fun to watch Richard Rusczyk’s solution. Turned out to be a lucky decision since his solution was totally different than the one we found:

It was neat to see this second solution – I learned a lot about 15-75-90 triangles today!

What a kid learning math can look like – similar triangles

My older son is reviewing geometry this summer using Art of Problem Solving’s Introduction to Geometry book. He’s been choosing pretty challenging problems for our movies, too. Today’s was a “star” problem in chapter 4. I thought his work was a nice illustration of what a kid learning about similar triangles can look like.

Here’s the introduction to the problem, some progress, and getting stuck:

Here’s the search for the second set of similar triangles. We end with a ration that will help us solve the problem, but we don’t go all the way to the end.

What a kid learning math can look like – congruent triangles

My older son is reviewing Art of Problem Solving’s Introduction to Geometry book this summer. Today he was working on problem relating to similar triangles, and the problem he picked for our movie was a fairly plain vanilla similar triangles problem:

The first part of the problem when smoothly, but the second part gave him some trouble. It was interesting to see his struggle to find the correct set of triangles to compare in the second part. Once you find them the problem is a snap – but finding them isn’t necessarily so easy when you are learning geometry. Staying with the problem might be the biggest lesson here.

Here are the two parts of our discussion today:

A neat tweet from Cilff Pickover

[sorry if this doesn’t read so well – this was my 6:00 am on the morning of daylight savings time exercise. We had to be out the door for something at 7:30, so I was a little rushed for time]

Saw a discussion about this tweet yesterday:

Shiver in ecstasy. The sides of a pentagon, hexagon, & decagon, inscribed in congruent circles, form right triangle. pic.twitter.com/Uastgc7SJo

— Cliff Pickover (@pickover) March 12, 2016

Last night I finally got around to checking out what was going on and ended up getting a fun surprise. Here’s how I approached the problem:

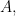
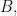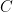I’ll let $A,$ $B,$ and $C$ be the sides of the triangle and use the law of cosines to find their length. Hopefully those lengths will satisfy the Pythagorean theorem. I’ll use degrees for the angle measures for reasons that will become clear below and let the radius of the three circles be 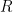$R$ . So . . .

$C^2 = 2R^2 - 2R^2 \cos(36)$ ,

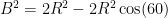$B^2 = 2R^2 - 2R^2 \cos(60)$ ,

$A^2 = 2R2 - 2R^2 \cos(72)$

Setting $A^2 + B^2 = C^2$ , a little algebra tells us that we have to have:

$\cos(36) - \cos(72) = 1/2$

This was the pleasant surprise, because I’d seen this exact problem before back in high school. In was problem 30 on the 1975 American High School Mathematics Exam (the AHSME):

Here’s a link to that test on Art of Problem Solving’s website:

The 1975 AHSME on Art of Problem Solving’s website

I remember running across this problem when I was reviewing old contests while studying to take the AHSME. This problem struck me because it taught me something really neat, and something that I thought then (and still do!) would be a really fun thing to show kids in trig class:

$\cos(36) = \frac{\sqrt{5} + 1}{4}$ and $\cos(72) = \frac{\sqrt{5} - 1}{4}$

The proof that I know is a really neat combination of algebra and geometry, and also a really neat illustration of mathematical thinking. For the particular problem of finding the value of 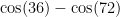$\cos(36) - \cos(72)$ there is an extra bit of fun math, too 🙂

Here’s a sketch of the argument.

Let 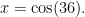$x = \cos(36).$ The double angle formula tells us that $\cos(72) = 2x^2 - 1,$ so the difference we are looking for is:

$-2x^2 + x + 1$ .

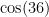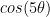We really don’t know anything about $\cos(36)$ other than that $\cos(5*36) = -1,$ so let’s see what the trig formulas tells us about $cos(5\theta)$ :

$\cos(5\theta) = \cos^5(\theta) - 10\cos^3(\theta)\sin^2(\theta) + 5\cos(\theta)\sin^4(\theta).$

A little algebra plus the identity $\sin^2(\theta) = 1 - \cos^2(\theta)$ gives us:

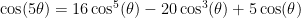
$\cos(5\theta) = 16\cos^5(\theta) - 20\cos^3(\theta) + 5\cos(\theta)$

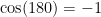Substituting $x = \cos(36)$ and $\cos(180) = -1$ we find that:

$16x^5 - 20x^3 + 5x + 1 = 0$

Now, I don’t want to spoil the geometric surprise, so I’ll just say that if you are interested in this problem marking the 5 angles on the unit circle that satisfy $\cos(5\theta) = -1$ is a good exercise. What do you notice?

That geometric exercise leads you to a nice algebraic observation – the above equation has one easy root and two pairs of double roots. This observation means that the above equation is surprisingly easy to factor:

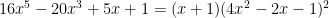
$16x^5 - 20x^3 + 5x + 1 = (x + 1)(4x^2 - 2x - 1)^2$

but that means that 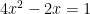$4x^2 - 2x = 1$ which we can re-write as 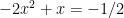$-2x^2 + x = -1/2$ . BUT, we were looking to find the value of:

$-2x^2 + x + 1$ , which we now know must be 1/2 !!! 🙂

That means the identity we found by applying the law of cosines to the triangle in Cliff Pickover’s tweet is indeed a right triangle. Yay!! Fun little problem.

As an aside, a couple of years ago I walked my older son through this argument just to show how some basic ideas in math can lead to pretty cool stuff. I didn’t expect him to understand every step, rather, I just wanted him to see the fun result that magically showed up again yesterday!

What learning math can look like: Guessing vs. Knowing

My older son and I looked at problem 19 from the 2014 AMC 10 b this morning:

He told me that he’d solved the problem correctly this morning and it seemed like a neat problem to talk about, so I wanted to hear his solution. It turned out that he had some good intuition, but not exactly a full solution:

So, after the rough argument that the answer was 1/3 I wanted him to try to find a more complete argument. Finding the right argument proved a little tough, so I asked him to go back to the information that came with the original problem. Using this information helped him find a more complete solution:

It was interesting to me to see the “hand waving” argument that showed the probability was likely to be around 1/3, and also instructive to see how much more work was required to find the complete solution. The whole process today gave me some insight into how kids think about the difference between thinking something is true and knowing something is true.

A neat question to share with a trig class from Mary Bourassa

Saw this question on Twitter from Mary Bourassa today:

What am I missing? Find side c first and get approx. 6.67. Then cosine law gives B = 96.7°, but w/ sine law B = 83°. pic.twitter.com/6ecOvaCIWw

— Mary Bourassa (@MaryBourassa) January 7, 2016

It is kind of cool to see what’s going on.

Here’s the first calculation using the law of cosines – we can see that the 3rd side does indeed equal roughly 6.67

We should be able to get the other two angles from the law of sines, but what happens when we look for the value of the angle opposite the side with length 11?

Since the law of sines only tells us the sine of the angle, we actually have two choices – which one is right? Let’s try 97 first:

Seems close enough – what happens when we check 83?

Dang, that doesn’t work at all. In fact, the side that has length 8 would have to have a length of about 9.6 to satisfy the law of sines.

But, are the two triangles related in some way? One cool relationship comes from the “extended law of sines” that says for any triangle:

A / Sin(a) = B / Sin(b) = C / Sin(c) = 2R, where R is the radius of the circumcircle.

We can check on Wolfram Alpha that the circumcircle for each of the two triangles has the same radius:

I have a soft spot for the extended law of sines because talking about it was one of the first videos that I ever put on youtube:

Here the extended law of sines tells us that although the two triangles have some different sides and angles, they can be inscribed in the same circle. Pretty neat 🙂

I think this would be a really fun problem to share with a trig class.

Patrick Honner’s angle problem

Last night Patrick Honner posted this introductory geometry problem on Twitter:

A nice, simple geometry problem with room to grow, as a mentor would say.#math #mathchat #geomchat pic.twitter.com/5A4iI1y4XU

— Patrick Honner (@MrHonner) November 16, 2015

I was looking for a problem to talk through with each of the kids this morning and this one fit the bill perfectly. It is a nice review problem for my older son and a nice way to (perhaps) introduce some new ideas to my younger son.

Also, the watching the two approaches to solving the problems is a nice illustration of the difference in approach that kids gain with a little experience (my older son is 2 years older than my younger son).

Here’s my older son’s approach to the problem. As this is more of a review problem for him, my goal is to have him carefully explain all of his steps:

Here’s my younger son’s approach. This is definitely not a review problem for him since he’s seen only a little bit of geometry. He knows a few basic ideas about angles and triangles, though, and he puts those ideas to use in his solution. The problem provided a nice opening for us to talk informally about angles and parallel lines, which was nice:

So, a luckily-timed tweet from Patrick Honner led to two nice conversations this morning. People sometimes look at me like I have four heads when I talk about all of the great math stuff that people share on Twitter, but here’s yet another example that led to some good conversations this morning!

More Patty Paper geometry + another viral math problem

Earlier this week Michael Pershan was asked for ideas about how to introduce constructions. One suggestion was using patty paper:

@mpershan Patty paper!!!!

— Ilana Horn (@ilana_horn) November 4, 2015

It has been a while since our first Patty Paper Geometry project, so I thought we’d give it another try 🙂

Flipping through the book last night I found a project in section 4.1 about finding the sum of angles in a polygon. I’d actually never seen this approach before and it looked really fun. We started with a triangle (and I’m sorry the pencil on the patty paper didn’t show up super well in the videos):

Next, as suggested by my younger son (and also in the book 🙂 ) we moved on to a quadrilateral:

Now we had a few conjectures and tried the same experiment with a pentagon to see if our conjectures held. It was pretty neat to hear the language (both in this video and in the last one) that the kids used to describe what was happening with the pentagon’s angles.

With that patty paper exercise as preparation, we looked at a viral geometry problem from last week. Here’s one link about the problem:

VCE Further Mathematics ‘50 cent’ question leaves Australian students confused

The problem gave the kids a bit of trouble – here’s their conversation about it:

I wanted the kids to puzzle about the problem a bit more, but they needed to head out the door, so I decided to simplify the picture for them so help them see what was going on:

So, a fun project. Using the patty paper to see why angles in a triangle add up to 180 degrees was really neat. As I said above, I’d never see the idea presented this way before. The extension to polygons with more sides was really natural and also led to some great conjectures from the kids.

I also enjoyed seeing the kids struggle with the 50 cent problem at the end. Not being around groups of kids working on math problems all that much, I usually have a difficult time knowing when (or why) problems will be difficult. Seeing the difficulty first had is always a great lesson.

A nice mental rotation problem from the 1988 AJHME

This problem from the 1988 AJHME gave my older son a little trouble today:

Problem 24 from the 1988 AJHME

We talked through it tonight and it turned out to be a really fun problem to talk through. It is surprisingly tricky to keep track of the rotations. Here are his initial thoughts about the problem, and you’ll see that he’s still having a bit of trouble with it:

Next we decided to make a hexagon and a square out of our Zometool set and actually make the rotations. That led to a fun conversation about what would happen if you rotated the square all the way around the hexagon:

Finally, I decided to try out the problem with my younger son and see if he had any different ideas. This was also an interesting conversation – especially when he wondered about what would happen if we rotated the square all the way around the hexagon:

So a fun little problem about mentally rotating a triangle around a square. Definitely a tough problem for kids to visualize, but a great problem to use to get them to talk about math.

Seeing angles and parallel lines for the first time

This week my younger son and I have started a new section in our Prealgebra about basic geometry. Today we talked about parallel lines and angles for the first time. The book had a pretty typical example problem of a someone (well, a chicken) changing direction while walking across the street and I thought it would be fun to see how my son would think about this problem having just started learning about lines and angles.

He’s obviously still an absolutely beginner when it comes to geometry, and some of the ideas that we’d normally take for granted – 180 degrees in a straight line, 360 degrees in a circle, for example – still trip him up a bit. But, he’s got a great way of thinking about math, and his 15 minute walk through this problem was fascinating to me.

In the first part of the discussion, he has some interesting ideas, but he applies one of the ideas about angles and parallel lines incorrectly and we don’t quite get to the correct solution:

In the second video we take a slightly deeper dive into angles and parallel lines to help him see the mistake in the prior video. He sees pretty quickly where he went wrong, and actually gives a great explanation of why the assumption he made wasn’t correct.

The last step was going back to the problem and looking for a new idea. Although we haven’t studied it, he’s heard that the angles in a triangle add up to 180 degrees, and the solution he finds to the problem uses that idea. I’m fine with that for now – we’ll cover triangles in more detail eventually.

I love watching kids learn and talk about math. It is so hard to put yourself back in their shoes and imagine what it is like seeing an idea for the very first time. I’m really happy with my son’s though process here. Especially since, once again we show that learning math isn’t always a nice, straight line.