Day: December 17, 2015

Using Matt Enlow’s shape division exercise with kids

Saw a great exercise tweeted out by Matt Enlow this morning:

Decided it would be fun to try out some of the exercises with my younger son who had a 1/2 day of school today. Hopefully this isn’t a spoiler to the worksheet – we only worked through the first two on camera!

My son loved the activity, though, and kept going after the camera was off. This is a amazing exercise to go through with kids!

Here’s the first exercise:

 

Here’s the second one:

 

A new algebra challenge

My son asked for another challenge problem today and I picked problem 16 from the 2015 AMC 10a:

Problem #16 from the 2015 AMC 10a

Here is the problem:

If 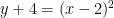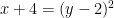y+4 = (x-2)^2 , x+4 = (y-2)^2, and x \neq y, what is the value of x^2+y^2?

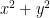I picked this problem because it was easy to state but required some careful algebra work. It took about 20 minutes to work through it completely. I hope the conversation is a good example of how a kid approaches problem solving.

Rather than jumping right into a solution, we started by looking at the problem and talking about a few different ways to approach it:

 

Having found two simplified versions of the equations in the problem at the end of the last video, we added them together to see what happened.

One interesting thing here is that my son thinks that we are on the right track because all of the choices in the problem are multiples of 5. However, not all numbers are integers!

 

We were a little stuck at the end of the last video. To try to get unstuck, we started this section by reviewing what we’d done so far.

Having had some success with adding the equations, my son thought that subtracting the two equations might be helpful. We gave that a try.

One important part of this section is the discussion about dividing by zero (or not dividing by zero, I guess):

 

Finally, to finish up the project we plugged in the two equations to Wolfram Alpha to get a better picture of what was going on. The picture helped my son see that there were four solutions to the two equations. He’d previously found the (5,5) solution, but had missed the (0,0) solution. Also, as I warned him about above, not all of the solutions were integers.

 

So, a nice algebra challenge. Maybe no individual step was super hard, but getting to the end of this problem involves a lot of algebra and a lot of problem solving ideas. Hopefully this was a good learning experience for him.