I’ll be giving two talks at math camps this summer. The first is at the east coast Idea math camp at the beginning of July and the second is at a math camp at Williams college in the middle of July.
I’m super excited to be able to have the opportunity to give these talks and can’t wait for the chance to interact with the students at the two camps.
The topics I’ll cover – not surprisingly – will come from some of the projects I’ve done with the boys this year. The talk at Williams is about 45 minutes shorter than the Idea math talk, so one or two of the topics below will get cut out.
Here’s are the ideas I’d like to cover:
(1) Larry Guth’s “No Rectangles” Problem
Larry Guth’s “No Rectangles” problem
I covered the 3×3 and 4×4 cases with the 2nd and 3rd graders at my younger son’s school as part of Family Math night and the kids loved the problem. With high school students I’d like to try to explore some of the larger cases and also discuss why this is a difficult problem for computers to solve.
Patrick Honner also showed me this related problem which I’ll leave as a challenge for the students 🙂
(2) Ann-Marie Ison’s Math Art
Our projects with Ann-Marie Ison’s art
I’m still waiting to hear what sort of projection capability I’ll have at the two events, but oh do I hope I have the ability to share this program with the students:
The explorations you can do with this simple modular arithmetic idea are incredible.
(3) A problem from Po-Shen Loh’s MoMath talk
What I love about Loh’s talk is that he takes an extremely difficult problem – one from the 2010 International Mathematics Olympiad – and turns it into a talk that is accessible to the public.
His approach is so accessible that I talked through the first part of the problem with my 4th grade son:
I’m very excited to hear the different guesses that the students have for the answer to Loh’s two questions.
(4) Bjorn Poonen’s N-Dimensional Sphere problem
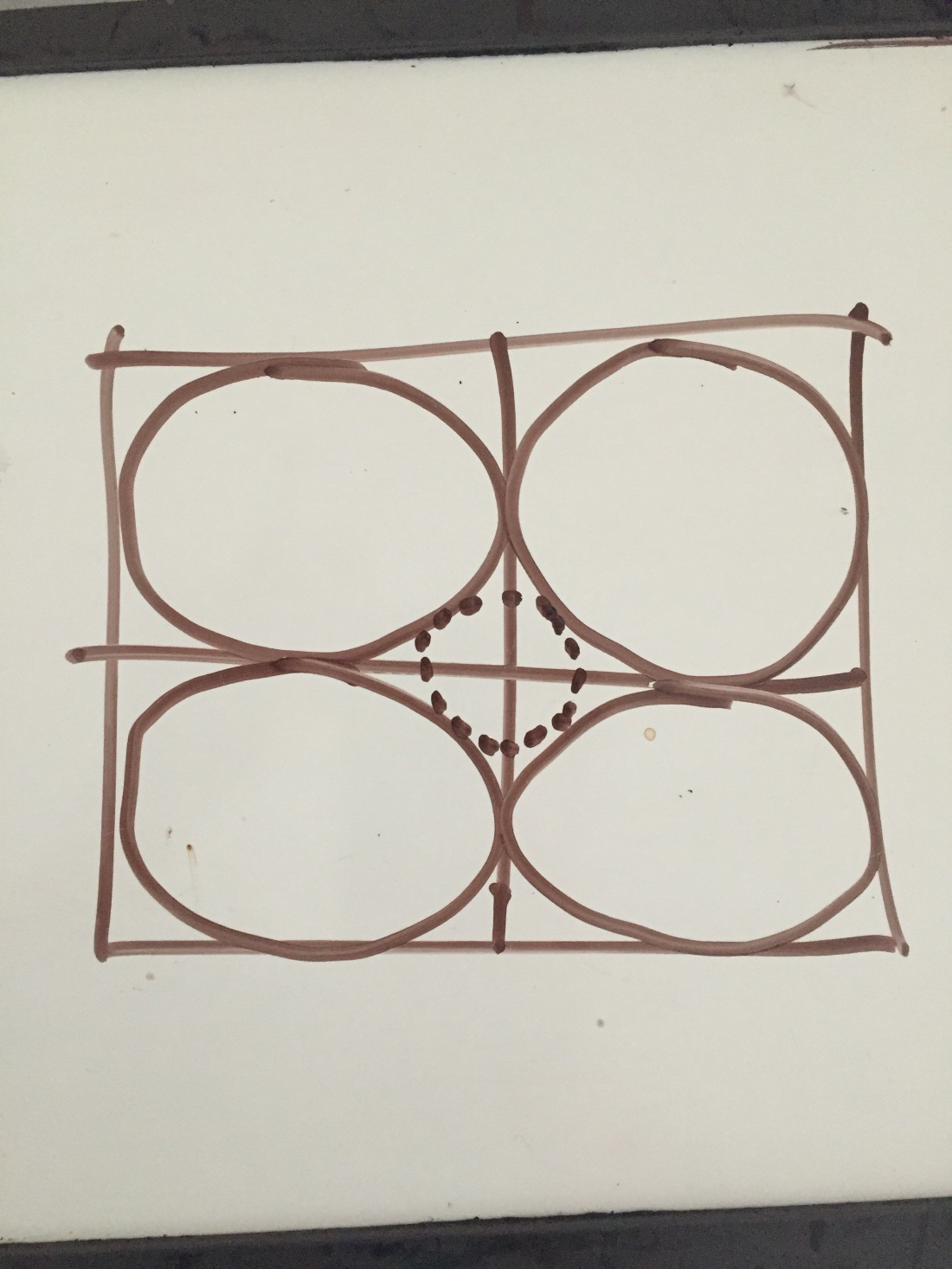
Here’s the problem and our project on the problem:
A strange problem I overheard Bjorn Poonen discussing
I’m guessing that not all of the kids will have seen geometry beyond 3 dimensions, so this problem will take a little bit of setting up. Luckily the only complicated bit of math that they need to understand it is the Pythagorean theorem and I’m guessing that all of them will know that theorem.
I was blown away by the answers to Poonen’s questions when I finally worked through them. This was also one of the most enjoyable projects that I’ve done with the boys this year.
I hope I have enough time to show the students the fun relationship between and
hiding in this problem, too:
A fun surprise in Bjorn Poonen’s n-dimensional sphere problem
Can’t wait to talk about these problems with the kids!
If you are ever in Seattle and want to give a talk to my math club send me an email. I’d love to host you.
I used to coach the Seattle women’s ultimate frisbee team Riot. I was there all the time 🙂